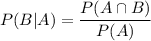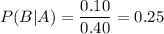Question

Samples of skin experiencing desquamation are analyzed for both moisture and melanin content. The results from 100 skin samples are as follows: melanin content high low moisture high 13 10 content low 47 30 Let A denote the event that a sample has low melanin content, and let B denote the event that a sample has high moisture content. Determine the following probabilities. Round your answers to three decimal places (e.g. 98.765).

a) P(A)
b) P(B)
c) P (A|B)
d) P (BA)

Answer 1

Answer: a. 0.40 b. 0.23 c . 0.435 d . 0.25

Explanation:

melanin content Total

high low

moisture high 13 10 23

content low 47 30 77

Total 60 40 100

Let A denote the event that a sample has low melanin content, and let B denote the event that a sample has high moisture content.

a) Total skin samples has low melanin content = 10+30=40

P(A)=
`(40)/(100)=0.40`

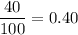
b) Total skin samples has high moisture content = 13+10=23

P(B) =
`(23)/(100)=0.23`

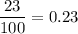
c) A ∩ B = Total skin samples has both low melanin content and high moisture content =10

P(A ∩ B) =
`(10)/(100)=0.10`

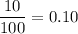
Using conditional probability formula ,
`P (A|B)=(P(A\cap B))/(P(B))`

`P (A|B)=(0.10)/(0.23)=0.434782608696\approx0.435`

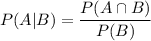
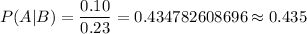
d)
`P (B|A)=(P(A\cap B))/(P(A))`

`P (B|A)=(0.10)/(0.40)=0.25`