Question

Leo invests $2,000 at an interest rate of 4%, compounded quarterly, and another $2,000 at an interest rate of 3.75%, compounded annually. How much are the investments worth in total at the end of 3 years?

Answer 1

Investments worth $4487.19 in total at the end of 3 years.

Solution:

Principal, P = 2000

Rate, R = 4% compounded quarterly

Rate, R = 3.75% compounded annually

Year, n = 3

Formula for compound interest when compounded quarterly:

`Amount=P(1+((R)/(4) )/(100))^(4n)`

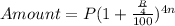
Substitute P = 2000, R = 4% and n = 3

`Amount=2000*(1+((4)/(4))/(100))^(4*3)`

`=2000*(1+(1)/(100))^(12)`

`=2000*((100+1)/(100))^(12)`

`=2000*((101)/(100))^(12)`

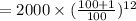
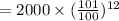
= 2253.65

Amount when compound interest calculated quarterly is 2253.65.

Formula for compound interest when compounded annually:

`Amount=P(1+(R)/(100))^(n)`

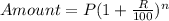
Substitute P = 2000, R = 3.75% and n = 3

`Amount=2000*(1+(3.75)/(100))^(3)`

`=2000*((100+3.75)/(100))^(3)`

`=2000*((103.75)/(100))^(3)`

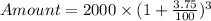
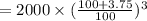
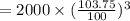
= 2233.54

Amount when compound interest calculated annually is 2233.54.

Total amount = 2253.65 + 2233.54

= 4487.19

Hence, investments worth $4487.19 in total at the end of 3 years.