Question

Which of the following are considered cylinders? Hint : Try to do this as if it were on the exam. Use the traces (or cross-sections) method to draw a picture to help you classify. (Click all that apply to get credit.)

A. 5y^{2}+2z^{2}=2

B. y=-\left(2x^{2}+2\right)

C. 5x^{2}+2y^{2}+4z^{2} = 5

D. 4x^{2}-4y^{2}+4z^{2} = 2

E. -\left(\cos\!\left(-4y\right)\right)=1-z

F. 2x^{2}+4y^{2}-4z = -1

G. None of the above.

Answer 1

Explanation:

A cylinder is a surface that consists of all lines (called rulings) that are parallel to a given line and pass through a given curve in some plane.

a)
`5y^(2)+2z^(2) = 2`

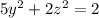
this is cylinder , this is ellipse in y-z plane ,but along x-axis ,we shall get the same curve in every possible plane parallel to the yz-plane.

b)
`y = -2x^(2) - 2`

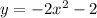
We have to be careful not to draw interpret it as an equation in 2-space even though there is no z - that just means it does not depend upon z. If we sketch this graph in the xy-plane (so z = 0, we obtain the parabola
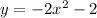`y = -2x^ 2 - 2`) . Since there is no z-value in the equation, we shall get the same curve in every possible plane parallel to the x-y-plane. In particular, the graph of this surface will be all vertical lines passing through the curvey = -2x^ 2 - 2 . in the xy-plane. By definition, this makes the graph a cylinder.

C)
`5x^(2)+2y^(2)+4z^(2) = 5`

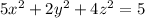
this is ellipsoid

`(x^2)/(a^2)+(y^2)/(b^2)+(z^2)/(c^2)=1`

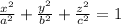
d)4x^(2)-4y^(2)+4z^(2) = 2

hyperboloid

`(x^2)/(a^2)+(y^2)/(b^2)-(z^2)/(c^2)=1`

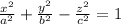
{x,y,z can be exchanged to each other}

e)1-z = - cos (-4y)

this is some curve in y-z plane ,so it is cylinder.

f)

2x^{2}+4y^{2}-4z = -1

elliptical paraboloid