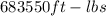To solve this problem we will use the work theorem, for which we have that the Force applied on the object multiplied by the distance traveled by it, is equivalent to the total work. From the measurements obtained we have that the width and the top are 14ft and 7ft respectively. In turn, the bottom of the tank is 15ft. Although the weight of the liquid is not given we will assume this value of
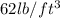 (Whose variable will remain modifiable until the end of the equations subsequently presented to facilitate the change of this, in case be different). Now the general expression for the integral of work would be given as
(Whose variable will remain modifiable until the end of the equations subsequently presented to facilitate the change of this, in case be different). Now the general expression for the integral of work would be given as
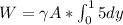
Basically under this expression we are making it difficult for the weight of the liquid multiplied by the area (Top and widht) under the integral of the liquid path to be equivalent to the total work done, then replacing
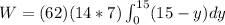
![W = (14*7*62)\big [15y-(y^2)/(2)\big ]^(15)_0](https://img.qammunity.org/2021/formulas/physics/college/nuzns6etz3mcixeqepe04xw7f0vn0atl89.png)
![W = (14*7*62)[15(15)-((15)^2)/(2)]](https://img.qammunity.org/2021/formulas/physics/college/yvuugrigewm7g3vmrp8blitb8g3bpm27kj.png)
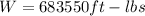
Therefore the total work in the system is