Answer:
(a) The gallons of water in a tub and the number of minutes since the tap was opened.
(c) The length of a side of a square and the perimeter of the square.
(d) The length of a side of a square and the area of the square.
Explanation:
Direct variation:
- When one quantity increases with the another quantity , they are said to be in direct proportion.
- An increase in one quantity leads to a proportional increase in another quantity, then, the quantity is said to vary directly with another.
- Mathematically, it can be expressed as:
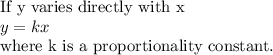
(a) The gallons of water in a tub and the number of minutes since the tap was opened.
As the minutes for which the tap is opened increases, there is an increase in the amount of water in tub.
Thus, there is a direct variation between the gallons of water in a tub and the number of minutes since the tap was opened.
(b) The height of a ball and the number of seconds since it was thrown.
As the time increases after the ball was thrown, its height increases. But after some time the height decreases and becomes zero.
Thus, this not an example of direct variation.
(c) The length of a side of a square and the perimeter of the square.
As the side of square increases the perimeter increases.
Thus, there is a direct variation between length of a side of a square and the perimeter of the square.
(d) The length of a side of a square and the area of the square.
As the side of square increases the area increases.
Thus, there is a direct variation between length of a side of a square and the area of the square.