Answer:
There are two such values of
 ,
,
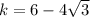 and
and

Explanation:
The question is to find all values of
 , if any, that satisfy the following matrix equation.
, if any, that satisfy the following matrix equation.
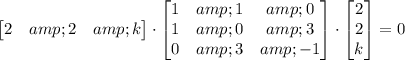
Let's multiply the first two matrices. We can do that, since the number of columns in the first matrix equals the number of rows in the second matrix, which means that their product is defined.
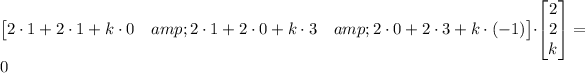
Next, we need to solve the matrix equation

Again, the number of columns in the first matrix equals the number of rows in the second matrix, which means that their product is defined and we can multiply them. The result will be
 ×
×
 matrix, and that will be the dimension of the zero matrix, as well.
matrix, and that will be the dimension of the zero matrix, as well.
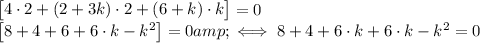
Now, all we need to do is to solve the quadratic equation
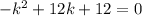
By using the well known formula, we obtain
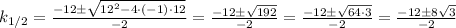
Therefore, we obtain two values for
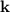 ,
,
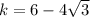 and
and
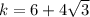 .
.