Question

How many ounces of a silver alloy that costs $5.50 per ounce should be mixed with one that costs $7.00 per ounce to make a new 30 ounce alloy that costs $6.40 per ounce?

Answer 1

135.73 ounces of a silver alloy that costs $5.50 per ounce should be mixed.

Explanation:

Given:

A silver alloy that costs $5.50 per ounce should be mixed with one that costs $7.00 per ounce to make a new 30 ounce alloy that costs $6.40 per ounce.

Now, to find the ounces of silver alloy.

Let the silver costs $5.50 per ounce be
`x.`

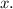
And the silver costs $7.00 per ounce be
`y.`

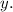
So, the total ounce make a new alloy:

`x+y=30\\y=30-x` ....(1)

Now, the total costs of silver alloy:

`5.50x+7y=6.4`

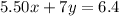
Putting the value of
`y` from equation (1) in the place of
`y` :

`5.50x+7(30-x)=6.4`

`5.50x+210-7x=6.4`

`-1.5x+210=6.4`

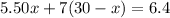
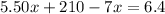
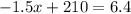
Subtracting both sides by 210 we get:

`-1.5x=-203.6`

Dividing both sides by -1.5 we get:

`x=135.73`

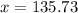
Therefore, 135.73 ounces of a silver alloy that costs $5.50 per ounce should be mixed.