Question

Given: KLMN is a parallelogram

m∠N=3m∠K,

LF

⊥

KN

,

LD

⊥

NM

KF=2 cm, FN=4 cm

Find: LF, LD


how to solve it

Answer 1

The value of LF is 2 cm and LD is 4.24 cm.

Explanation:

Given :Parallelogram KLMN

LF ⊥ KN

LD ⊥ NM

KF = 2 cm, FN = 4 cm

∠N = 3∠K

To find : LF , LD

Solution :

Sum of all angles of parallelogram is 360°.

∠N + ∠K +∠L + ∠M = 360°

∠N + ∠K +∠N + ∠K = 360° (opposites angles are equal in ||gram)

∠3K + ∠K +∠3K + ∠K = 360°

8∠K=360°

∠K = 45°

In triangle KLF

`\tan 45^o=(LF)/(KF)`

`1=(LF)/(2 cm)`

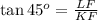
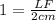
LF = 2 cm

In triangle LMD

LM = KN = 6 cm (Opposites sides are equal in ||gram)

`\Sin 45^o=(LD)/(LM)`

`0.7071 =(LD)/(6 cm)`

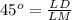
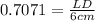
LD = 4.24 cm (approx)

The value of LF is 2 cm and LD is 4.24 cm.