Answer:
a)
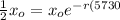
We can cancel
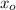 and we got:
and we got:
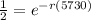
We apply natural log and we got:
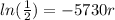
And
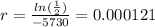
b)
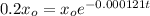
We can cancel
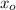 in both sides and we got:
in both sides and we got:
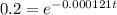
Now we can apply natural log on both sides and we got:
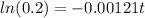
And if we solve for t we got:
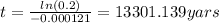
So in order to have 20% of the original amount
 the total time is 13301.14 years approximately.
the total time is 13301.14 years approximately.
Explanation:
Part a
For this case we have the following model given by the differential equation:
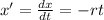
The solution for this model is given by:
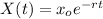
Using the half life we know that for 5730 years we need to have 1/2 of the initial amount
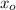 so if we replace we have this:
so if we replace we have this:
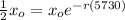
We can cancel
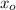 and we got:
and we got:
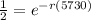
We apply natural log and we got:
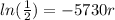
And
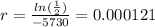
Where
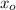 represent the initial amount. For this case we know the value for the rate of decay
represent the initial amount. For this case we know the value for the rate of decay
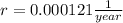
Part b
And the half like is 5730 years. And we want to find the time in years in order to have 20% of the original amount. So we can write the following expression:
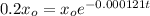
We can cancel
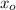 in both sides and we got:
in both sides and we got:
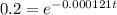
Now we can apply natural log on both sides and we got:
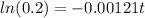
And if we solve for t we got:
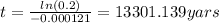
So in order to have 20% of the original amount
 the total time is 13301.14 years approximately.
the total time is 13301.14 years approximately.