Question

Two rockets are launched at a fireworks display. Rocket A is launched with an initial velocity v0 5 100 m/s and rocket B is launched t1 seconds later with the same initial velocity. The two rockets are timed to explode simultaneously at a height of 300 m as A is falling and B is rising. Assuming a constant acceleration g 5 9.81 m/s2, determine (a) the time t_1, (b) the velocity of B relative to A at the time of the explosion.

Answer 1

given,

initial speed of the rocket A = 100 m/s

height of explode = 300 m

acceleration due to gravity = 9.8 m/s²

rocket b is launched after t₁ time

now, using equation of motion to calculate time

`s = ut + (1)/(2)gt^2`

`300 = 100t + (1)/(2)(-9.8)t^2`

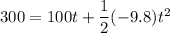
4.9 t² - 100 t + 300 = 0

using quadratic equation

`t = (-(-100)\pm √(100^2-4* 4.9 * 300))/(2* 4.9)`

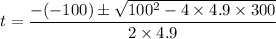
t₁ = 3.65 s and t₂ = 16.75 s

now, rocket A reaches 300 m on return at 16.75 s

rocket B reaches 300 m after 3.65 s

time difference of launch:

t = 16.75 - 3.65

t = 13.1 s

velocity of rocket A

v_a = u + g t

v_a =100 - 9.8 x 16.75

v_a = -64.15 m/s

velocity of rocket B

v_b = u + g t

v_b =100 - 9.8 x 3.65

v_b =+64.23 m/s

relative velocity of B relative to A at the time of the explosion

`V_(BA) = v_b - V_a`

`V_(BA) = 64.23 -(-64.15)`

`V_(BA) = 128.38\ m/s`

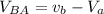
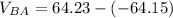
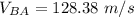
relative velocity is equal to 128.38 m/s