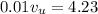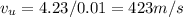Answer:
423m/s
Step-by-step explanation:
Suppose after the impact, the bullet-block system swings upward a vertical distance of 0.4 m. That's means their kinetic energy is converted to potential energy:
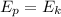
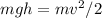
where m is the total mass and h is the vertical distance traveled, v is the velocity right after the impact at, which we can solve by divide both sides my m
Let g = 9.81 m/s2
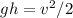
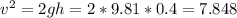
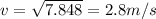
According the law of momentum conservation, momentum before and after the impact must be the same
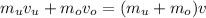
where
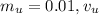 are the mass and velocity of the bullet before the impact, respectively.
are the mass and velocity of the bullet before the impact, respectively.
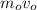 are the mass and velocity of the block before the impact, respectively, which is 0 because the block was stationary before the impact
are the mass and velocity of the block before the impact, respectively, which is 0 because the block was stationary before the impact