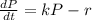Answer:
A) Differential equation for population growth in case of individual immigration is:

B) Differential equation for population growth in case of individual emigration is:
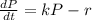
Explanation:
Population growth rate in the absence of immigration and emigration is given as:
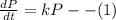
A) When individuals are allowed to immigrate:
Let r be the constant rate of individual immigration given that r >0.
Differential equation for population growth in this case is:

B) In case of individual emigration:
Let r be the constant rate of individual emigration given that r >0.
Differential equation for population growth in this case is: