Answer:
Flow rate 2.34 m3/s
Diameter 0.754 m
Step-by-step explanation:
Assuming steady flow, the volume flow rate along the pipe will always be constant, and equals to the product of flow speed and cross-section area.
The area at the well head is
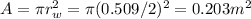
So the volume flow rate along the pipe is
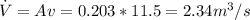
We can use the similar logic to find the cross-section area at the refinery
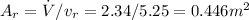
The radius of the pipe at the refinery is:
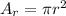
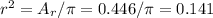
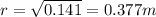
So the diameter is twice the radius = 0.38*2 = 0.754m