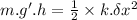Answer:
a)
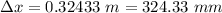
b)
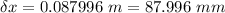
c)

Step-by-step explanation:
Given:
- mass of the object,
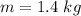
- height of the object above the spring,

- spring constant,
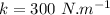
a)
When the object is dropped onto the spring whole of the gravitational potential energy of the mass is converted into the spring potential energy:
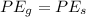

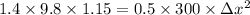
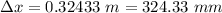 is the compression in the spring
is the compression in the spring
b)
When there is a constant air resistance force of 0.6 newton then the apparent weight of the body in the medium will be:
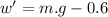

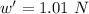
Now the associated gravitational potential energy is converted into the spring potential energy:
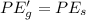
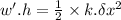
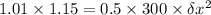
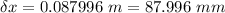
c)
On moon, as per given details: