Question

The line passing through (11,y) and (2,0) is parallel to the line joining (7,5) and (-2,2). Find y.

Answer 1

y=3

Explanation:

Lets set 4 points A(11,
`y_(1)`), B(2,0), C(7,5), D(-2,2)

So first we need to find a line that passes through points C and D

`\left \{ {{a*7+b=5} \atop {a*(-2)+b=2}} \right.`

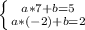
We subtract these two

9a=3

a=3/9

a=1/3

b=2+2*
`(1)/(3)`

b=8/3

So the line passing through C and D is
`(1)/(3)x+(8)/(3)=y`

We do the same for the line passing through A and B

`\left \{ {{a*11+b=y_(1)} \atop {a*2+b=0}} \right.`

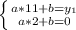
9*a+y

Line AB and line CD will be paraller if
`a_(1)= a_(2)`

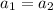
So from that we know that a=1/3

So 9*(1/3)=3=y