Question

PlEASEHELP AND PLSSS CAMN YALL HELP

Find point Z that partitions the directed line segment XY in the ratio of 5:3 where X(-2, 6) and Y(-10, -2).

Answer 1

The coordinates of point Z are (–7, 1).

Solution:

Given data: X(–2, 6) and Y(–10, –2)

Point Z partitions the line segment XY in the ratio 5:3.

XZ : ZY = 5 : 3

X(–2, 6) can be taken as
`X(x_1, y_1)`.

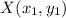Y(–10, –2) can be taken as
`Y(x_2, y_2)`.

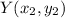XZ : ZY can be taken as m : n = 5 : 3.

We know that coordinate of point
`Z(x_3, y_3)` divides line segment joining
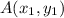`A(x_1, y_1)` and
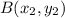`B(x_2, y_2)` in ratio m : n is

`Z(x_3,y_3)=((mx_2+nx_1)/(m+n), (my_2+ny_1)/(m+n))`

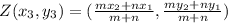
Here,
`x_1 = -2, x_2=-10, y_1=6, y_2=-2` and m = 5, n = 3.

Substitute these in the above formula, we get,

`Z\left(x_(3), y_(3)\right)=\left((5 *(-10)+3 *(-2))/(5+3), (5 *(-2)+3 *(6))/(5+3)\right)`

⇒
`=\left((-50-6)/(8), (-10+18)/(8)\right)`

⇒
`=\left((-56)/(8), (8)/(8)\right)`

⇒
`Z\left(x_(3), y_(3)\right)=(-7,1)`

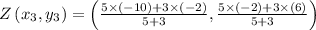
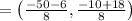
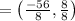
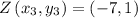
Hence the coordinates of point Z are (–7, 1).