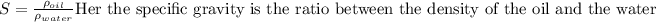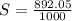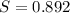To solve this problem we will apply the theoretical concepts and definitions given for the specific weight, density and specific gravity. Consider also that a barrel contains 159 liters or
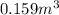
Consider the net weight of the oil which would be
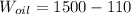
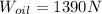
The specific weight is defined as the proportion of weight by volume thereof, therefore

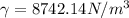
Through the information given we could find mass and density through the following relations:
Mass
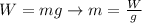
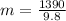

Density
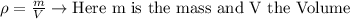
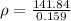
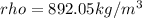
Specific gravity,