Question

Network breakdowns are unexpected rare events that occur every 3 weeks, on the average. Compute the probability of more than 4 breakdowns during a 21-week period

Answer 1

0.827

Explanation:

Data provided in the question:

Probability of breakdown, p = once in 3 weeks i.e
`(1)/(3)`

number of weeks n = 21

now,

mean, λ = np

=
`(1)/(3)*21`

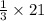
= 7

P(X > 4) = 1 - ( P(X ≤ 4))

using Poisson distribution

P(X = x) =
`(e^(-\lambda)\lambda^x)/(x!)`

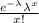
Thus,

P(X = 0) =
`(e^(-7)7^0)/(0!)`

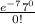
= 0.00091

P(X = 1) =
`(e^(-7)7^1)/(1!)`

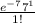
= 0.00638

P(X = 2) =
`(e^(-7)7^2)/(2!)`

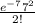
= 0.02234

P(X = 3) =
`(e^(-7)7^3)/(3!)`

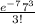
= 0.05213

P(X = 4) =
`(e^(-7)7^4)/(4!)`

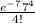
= 0.09123

Thus,

P(X ≤ 4) = P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3) + P(X = 4)

= 0.00091 + 0.00638 + 0.02234 + 0.05213 + 0.09123

= 0.17299

Therefore,

P(X > 4) = 1 - 0.17299

= 0.827