Question

In my friend's coin purse, I found 12 pennies. The ages, in years, of the pennies obtained by subtracting the year stamped on the coin from 2016 follow. 22, 14, 8, 1, 9, 0, 31, 2, 13, 3, 11, 10 Rounding to the nearest tenth, the mean and median of this distribution (in years) are:a. mean = 11.3 and median = 9.5b. mean = 10.3 and median = 10.5c. mean = 10.3 and median = 9.5d. mean = 9.5 and median = 10.3e. mean = 10.3 and median = 8.5

Answer 1

Answer: mean = 10.3 and median = 9.5

Explanation:

Given data :

22, 14, 8, 1, 9, 0, 31, 2, 13, 3, 11, 10

Mean =
`\frac{\text{Sum of all data values}}{\text{No. of data values}}`

`=(22+14+8+1+9+0+31+2+13+3+11+10)/(12)`

`=(124)/(12)=10.3`

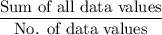
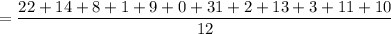
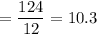
Median = Middle most value.

For Median , we first arrange the data values in an order.

0 , 1 , 2, 3, 8, 9, 10 , 11, 13 , 14, 22, 31

Since , number of data values is 12 ( even) , so the median would be the mean of the two middlemost value.

i.e . Median=
`(9+10)/(2)=9.5`

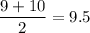
Hence, the mean and median of this distribution (in years) are :

mean = 10.3 and median = 9.5