Question

If n denotes a number to the left of 0 on the number line such that the square of n is less than
`\small (1)/(100)`, then the reciprocal of n must be _________.

Answer 1

The reciprocal of n must be less than –10

Solution:

Given n denotes a number to the left of 0 means n < 0.

Square of n is less than
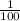`(1)/(100)` means
`n^2<(1)/(100)`.

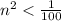Therefore, we have
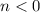`n<0` and
`n^2<(1)/(100)`.

⇒
`n^2<(1)/(100)`

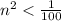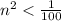
Taking square root on both sides, we get

⇒
`n<\± (1)/(10)`

⇒
`(-1)/(10)<n<(1)/(10)`

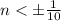
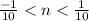
⇒ But we know that n < 0, so
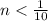`n<(1)/(10)` false.

It should be
`(-1)/(10)<n`.

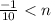To equal the expression, multiply both sides of the equation by –10n.

⇒
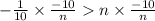`-(1)/(10) *(-10)/(n)>n *(-10)/(n)` (symbol < changed to > when multiply by minus)

⇒
`(1)/(n)>-10`

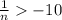
Hence, the reciprocal of n must be less than –10.