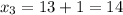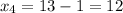Question

Unless otherwise specified in the question, responses to numerical question must be within 5% of the correct answer. Try out different responses to the following question, which has an answer of 20, where a correct response is between 19 and 21.

What is the average velocity (in kilometers per hour) of a cart that travels 100 km in 5 hours?

2.An exception to the 5% tolerance rule arises for simple calculations that can be done in your head that come out as integers or or simple decimals. So if the calculation involves dividing 5 by 2 with the result of 2.5, an answer of 2.6 may not be graded as correct.

Give the value of 6.5 times 2.

Try it several times giving the answer (13) in different forms (say, 13 or 1.3e1) and with different accuracies (say, 13.001 or 13.2). Since this is a simple calculation, two of these four will be graded as incorrect.

Answer 1

Part of the problem involves not only answering the question with the correct degree of accuracy, but also making approximations to the correct answer. For example, for the first case we know that the speed is equivalent to the distance traveled in a given time. Therefore it would be defined as

]1)
`V = (x)/(t)`

x = Displacement

t = Time

The displacement value is 100km and the time value is 5 hours. Therefore the speed value would be

`V = (100km)/(5h) = 20km/h`

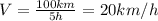
We know that the answer margin is within 5% of the value, then 5% of 20 would be 1. That is, we have a margin of error of '1km / h' to answer the question. Any value that falls within that range can be added or subtracted from the response and the response will be valid. Values included within this value would be

`V_1 = 20km/h +1km/h = 21km/h`

`V_2 = 20km/h - 1km/h = 19km/h`

`V_3 = 20km/h + 0.5km/h = 20.5km/h`

`V_4 = 20km/h -0.5km/h = 19.5km/h`

`V_5 = 20km/h +0.01km/h = 20.01km/h`

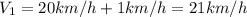
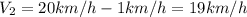
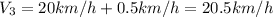
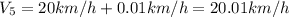
2) For the second case the margin of tolerance for the response is 5%, so if we multiply the given value we would have a response of.

`x = 6.5*2 = 13`

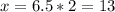
5% of 13 is 0.65. Therefore, any value that falls within that range will be a correct answer. The value could then be

`x_1 = 13+0.65 = 13.65`

`x_2 = 13-0.65 =12.35`

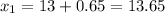
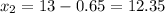
Incorrect values will be

`x_3 = 13+1 = 14`

`x_4 = 13-1=12`