Question

solve the below systems of equations using linear combination method. 2x + 3y =1. and y= -2x - 9. explain

Answer 1

Solving below systems of equations using linear combination method we get

x = -7

y = 5

Explanation:

Linear combinations which is also commonly known as the addition method is used for solving the system of equations without graphs

Step 1: arrange the equation in standard form

2x + 3y = 1----------------------(1)

2x + y = -9--------------------(2)

Step 2: Set one of the coefficient to opposite sides

So lets multiply eq(2) with negative sign, so

2x + 3y = 1

-2x - y = 9

Step 3: Perform Addition

2x + 3y = 1

-2x - y = 9

-----------------------

0x +2y = 10

--------------------------

Step 4: Solve for y

2y =10

`y =(10)/(2)`

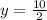
y = 5

Step 5: Substitute y value in equation(1)

2x + 3(5) = 1

2x + 15 =1

2x = 1-15

2x =-14

`x= (-14)/(2)`

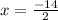
x = -7