Question

An arrow is shot from a height of 1.95 m toward a cliff of height H. It is shot with a velocity of 29 m/s at an angle of 60° above the horizontal. It lands on the top edge of the cliff 3.8 s later.

a) What is the height of the cliff (in m)?

(b) What is the maximum height (in m) reached by the arrow along its trajectory?

(c) What is the arrow's impact speed (in m/s) just before hitting the cliff?

Answer 1

a) H = 26.63 m.

b)
`y_(max) = 34.13~m`

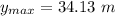
c) v = 18.89 m/s.

Step-by-step explanation:

a) We will use kinematics equations for 2D-projectile motion.

First we will separate the velocity into x- and y-components, and apply the kinematics equations separately.

y-direction:

`y - y_0 = v_(y_0)t + (1)/(2)at^2\\H - 1.95 = (29\sin(60))(3.8) + (1)/(2)(-9.8)(3.8)^2\\H = 26.63~m`

b) Another kinematics equation will help us to find the maximum height.

`v_y^2 = v_(y_0)^2 + 2a(\Delta y)\\0 = (29\sin(60))^2 + 2(-9.8)(y_(max) - 1.95)\\y_(max) = 34.13~m`

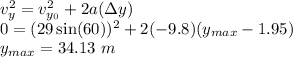
c) The impact speed is the sum of the speed in both directions.

`v_y^2 = v_(y_0)^2 + 2a(H-y_0)\\v_y^2 = (29\sin(60))^2 + 2(-9.8)(26.63 - 1.95)\\v_y = 12.12~m/s`

`v_x^2 = v_(x_0)^2 + 2a_x(\Delta x)\\v_x^2 = (29\cos(60))^2 + 2(0)(\Delta x)\\v_x = 14.5~m/s`

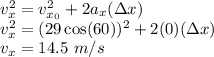
The impact speed is

`v = √(v_x^2 + v_y^2) = √(14.5^2 + 12.12^2) = 18.89~m/s`