Question

What is the value of the composite constant (Gme,/r2e) to be multiplied by the mass of the object mo, in equation below:

Fg=G(mem0/r2e)=(Gme/r2e)mo

mo=object of mass sitting on surface, me=mass of earth, re=distance between object and center of earth

earth has mass m earth=5.98 x 1024 kg, sun has mass m sun=1.99 x 1030 kg,

r=93 million miles=150 million km

Answer 1

To solve this problem we will apply the definitions given in Newtonian theory about the Force of gravity, and the Force caused by weight. Both will be defined below, and in equal equilibrium condition to clear the variable concerning acceleration due to gravity. Finally, with the values provided in the statement, it will be replaced.

The equation for the gravitational force between the Earth and the object on the surface of the Earth is

`F_g = (Gm_em_o)/(r^2_e)`

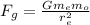
Where,

G = Universal gravitational constant

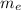`m_e` = Mass of Earth

`r_e`= Distance between object and center of earth

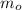`m_o`= Mass of Object

The equation for the gravitational pulling force on the object due to gravitational acceleration is

`F_g = m_o g`

Equation the two expression we have

`m_o g = (Gm_em_o)/(r_e^2)`

`g = (Gm_e)/(r_e^2)`

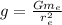
This the acceleration due to gravity which is composite constant.

Replacing with our values we have then

`g = ((6.67*10^(-11)N\cdot m^2/kg^2)(5.98*10^(24)kg))/(6378km((10^3m)/(1km))^2)`

`g = 9.8m/s^2`

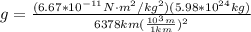
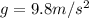
The value of composite constant is
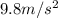`9.8m/s^2`. Here, the composite constant is nothing but the acceleration due to gravity which is constant always.