Answer: 90
Explanation:
The formula for calculating the nth term of a sequence is given as :
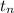= a + ( n - d )
Where a is the first term
d is the common difference and
n is the number of terms
This means that the 4th term of an arithmetic sequence will have the formula :
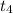= a + 3d
And the 4th term has been given to be , 12 ,substituting into the formula we have
12 = a + 3d .............................. equation 1
Also substituting for the 8th term , we have
36 = a + 7d .............................. equation 2
Combining the two equations , we have
a + 3d = 12 ................... equation 1
a + 7d = 36 ------------ equation 2
Solving the system of linear equation by substitution method , make a the subject of formula from equation 1 , that is
a = 12 - 3d ................... equation 3
substitute a = 12 - 3d into equation 2 , equation 2 then becomes
12 - 3d + 7d = 36
12 + 4d = 36
subtract 12 from both sides
4d = 36 - 12
4d = 24
divide through by 4
d = 6
substitute d = 6 into equation 3 to find the value of a, we have
a = 12 - 3d
a = 12 - 3 ( 6)
a = 12 - 18
a = -6
Therefore , the 17th term of the sequence will be :
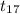= a + 16d
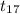= -6 + 16 (6)
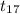= -6 + 96
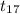= 90
Therefore : the 17th term of the sequence is 90