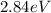Question

Sodium and mercury are currently used in lighting applications. The peak emissions are at 589 nm (yellow) and 436 nm (blue), respectively. What are the corresponding energy and frequency values in eV and Hertz, respectively

Answer 1

Answer : The energy and frequency of yellow and blue peak is, 2.10 eV,
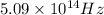`5.09* 10^(14)Hz` and 2.84 eV,
`6.88* 10^(14)Hz` respectively.

Explanation :

Part 1:

Given:

Wavelength of yellow peak =
`589nm=589* 10^(-9)m`

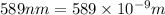
Conversion used :
`1nm=10^(-9)m`

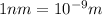
First we have to calculate the frequency of yellow peak.

Formula used :

`\\u=(c)/(\lambda)`

where,

`\\u` = frequency of yellow peak

`\lambda` = wavelength of yellow peak

c = speed of light =
`3* 10^8m/s`

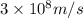
Now put all the given values in the above formula, we get:

`\\u=(3* 10^8m/s)/(589* 10^(-9)m)`

`\\u=5.09* 10^(14)s^(-1)=5.09* 10^(14)Hz`
`(1Hz=1s^(-1))`

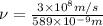
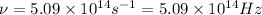
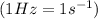
The frequency of yellow peak is,
`5.09* 10^(14)Hz`

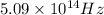
Now we have to calculate the energy of yellow peak.

Formula used :

`E=h* \\u`

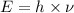
where,

`\\u` = frequency of yellow peak

h = Planck's constant =
`6.626* 10^(-34)Js`

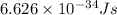
Now put all the given values in the above formula, we get:

`E=(6.626* 10^(-34)Js)* (5.09* 10^(14)s^(-1))`

`E=3.37* 10^(-19)J`

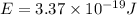
Also,

`1J=6.24* 10^(18)eV`

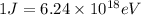
So,

`Energy=(3.37* 10^(-19))* (6.24* 10^(18)eV)`

`Energy=2.10eV`

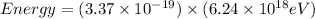
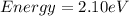
The energy of yellow peak is
`2.10eV`

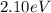
Part 2:

Given:

Wavelength of blue peak =
`436nm=436* 10^(-9)m`

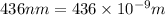
Conversion used :
`1nm=10^(-9)m`

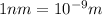
First we have to calculate the frequency of blue peak.

Formula used :

`\\u=(c)/(\lambda)`

where,

`\\u` = frequency of blue peak

`\lambda` = wavelength of blue peak

c = speed of light =
`3* 10^8m/s`

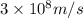
Now put all the given values in the above formula, we get:

`\\u=(3* 10^8m/s)/(436* 10^(-9)m)`

`\\u=6.88* 10^(14)s^(-1)=6.88* 10^(14)Hz`
`(1Hz=1s^(-1))`

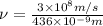
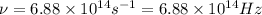
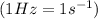
The frequency of blue peak is,
`6.88* 10^(14)Hz`

Now we have to calculate the energy of blue peak.

Formula used :

`E=h* \\u`

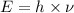
where,

`\\u` = frequency of blue peak

h = Planck's constant =
`6.626* 10^(-34)Js`

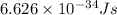
Now put all the given values in the above formula, we get:

`E=(6.626* 10^(-34)Js)* (6.88* 10^(14)s^(-1))`

`E=4.56* 10^(-19)J`

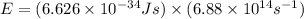
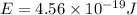
Also,

`1J=6.24* 10^(18)eV`

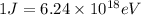
So,

`Energy=(4.56* 10^(-19))* (6.24* 10^(18)eV)`

`Energy=2.84eV`

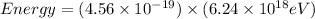
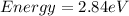
The energy of blue peak is
`2.84eV`