Answer:
The probability that the reservoir will be empty in the next ten days is 0.476
Explanation:
In 10 days, the reservoir will have 10000 units of water depleted. Since the reservoir starts with almost 5000, then by gaining 8000 units it wont get emptied. It also wont get emptied if it gains 5000 or more units twice, thus, if it rains during 2 days it shoudnt get emptied.
However, note that the reservoir could get emptied if it doesnt rain in the first five days, because it will lose 5000 units, exceding its starting amount. Thus, there are only 2 possibilities for the reservoir to be emptied:
- If it doesnt rain in the first five days
- If it rains only once in the fisrt five days providing only 5000 units of water, and during the second period of five days it doesnt rain.
We know that the rainfall distribution is Poisson with rate 0.2 per day. In five days the rate is 0.2*5 = 1; lets call X this random variable. The probability to not have any rainfalls in 5 days is
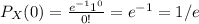
Also, the probability for it to rain just once in five days is the probability of X being equal to one
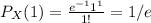
Therefore, the probability of the event 'it doesnt rain in the first five days' is 1/e, and the probability of the other event 'it rains once in the first five days, also that rain adds 5000 units of water and it doesnt rain in the other five days' is
1/e*0.8*1/e (we multiply 1/e foe the probability that the rain gives 5000 units of water and then by the probability that it doesnt rain in the last five days).
Summing both disjoint events, we obtain that the probability that the reservoir is emptied is
1/e+ 1/e*0.8*1/e = 0.476