Question

HELP ASAP!! A toy rocket is launched from a platform 36 feet above the ground at a speed of 97 feet per second. The height of the rocket in feet is given by the polynomial −16t^2 + 97t + 36, where t is the time in seconds. How high will the rocket be after 3 seconds?

Answer 1

The height of the rocket after 3 seconds = 183 feet

Explanation:

Given:

Rocket is initially launched from a height of 36 feet.

Initial speed of the rocket = 97 ft/s

The height of the rocket at any time
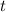`t` in seconds is given as:

`-16t^2+97t+36`

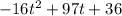
To find the height of the rocket after 3 seconds.

Solution:

The height function of the rocket is:

`h(t)=-16t^2+97t+36`

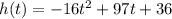
In order to find the height of the rocket after
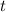`t` seconds we plugin
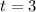`t=3` in the function.

`h(3)=-16(3)^2+97(3)+36`

`h(3)=-16(9)+291+36`

`h(3)=-144+291+36`

`h(3)=183\ ft`

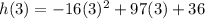
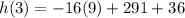
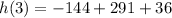
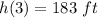
Thus, height of the rocket after 3 seconds = 183 feet.