Option A:
Hence, x ÷ 4 > x – 12 is true for x = 20.
Solution:
To find which is the suitable inequality is true for the value x = 20.
Option A: x ÷ 4 > x – 12
⇒
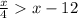
Multiply 4 on both sides of the inequality,
⇒ x > 4x – 48
Subtract 4x on both sides of the inequality,
⇒ –3x > – 48
⇒ 3x > 48
Divide 3 on both sides,
⇒ x > 16
If x = 20, then 20 > 16 is true.
Option B: 2x < x +22
Subtract x on both sides of the inequality,
⇒ x < 22
If x = 20, then 20 < 22 is false.
Option C: x + 30 > 3x
Subtract x on both sides of the inequality,
⇒ 30 > 2x
Divide by 2 on both sides of the inequality,
⇒ 15 > x
If x = 20, then 15 > 20 is false.
Option D: x – 5 < 2x – 35
Subtract x on both sides of the inequality,
⇒ – 5 < x – 35
Add 35 on both sides of the inequality,
⇒ 30 < x
If x = 20, then 30 < 20 is false.
Hence, x ÷ 4 > x – 12 is true for x = 20.