Question

An astronaut is on a 100-m lifeline outside a spaceship, circling the ship with an angular speed of

0.100 rad/s. How far inward can she be pulled before the centripetal acceleration reaches 5g = 49 m/s2?

Answer 1

D = 72.68 m

Step-by-step explanation:

given,

R = 100 m

angular speed = 0.1 rad/s

distance she can be pulled before the centripetal acceleration reaches 5g = 49 m/s².

using conservation of Angular momentum

`I_i\omega_i= I_f\omega_f`

`mr_i^2\omega_i=m r_f^2\omega_f`

`\omega_f = (r_i^2)/(r_f^2)* \omega_i`

`\omega_f = (r_i^2)/(r_f^2)* \omega_i`

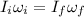
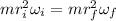
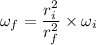
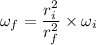
we know,

centripetal acceleration

`a = (v^2)/(r)`

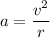
v = r ω

`a =\omega_f^2 r_f`

`a =((r_i^2)/(r_f^2)* \omega_i)^2 r_f`

`a =(r_i^4* \omega_i^2)/(r_f^3)`

`r_f^3=(100^4* 0.1^2)/(5* 9.8)`

`r_f^3=20408.1632`

`r_f = 27.32\ m`

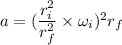
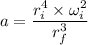
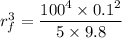
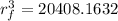
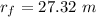
distance she has reached inward is equal to

D = 100 - 27.23

D = 72.68 m