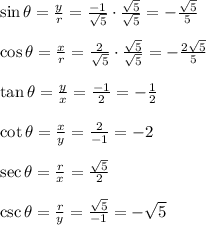Question

Find the six trigonometric function values of the angle θ in standard position, if the terminal side of θ is defined by x + 2y = 0, x ≥ 0.

Answer 1

`\sin \theta = \frac{y}r} = (-1)/(√(5)) \cdot (√(5))/(√(5)) = -(√(5))/(5)\\\\\cos \theta = (x)/(r) = (2)/(√(5)) \cdot (√(5))/(√(5)) = -(2√(5))/(5) \\\\\tan \theta = (y)/(x) = (-1)/(2) = -(1)/(2) \\\\\cot \theta = (x)/(y) = (2)/(-1) = -2\\\\\sec \theta = (r)/(x) = (√(5))/(2) \\\\\csc \theta = (r)/(y) = (√(5))/(-1) = -√(5)`

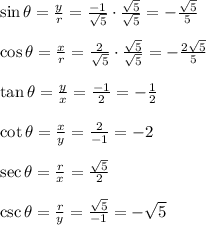
Explanation:

First, we need to draw the terminal position of the given angle. To do so, we need to find a point that lies on the straight line
`x + 2y= 0, x\geq 0`

If we choose
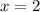`x = 2` (we can do so because of the condition
`x \geq 0`, which means that any positive value is suitable for
`x`), then we have

`2 +2y = 0\implies 2 = -2y \implies y = -1`

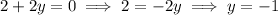
Therefore, the terminal side of the angle
`\theta` is passing through the origin and the point
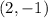`(2,-1)` and now we can draw it.

The angle
`\theta` is presented below.

The distance of the point
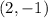`(2,-1)` from the origin equals

`r = √(2^2 + (-1)^2) = √(5)`

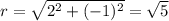
Now, we can determine the values of the six trigonometric function, by using their definitions.

`\sin \theta = \frac{y}r} = (-1)/(√(5)) \cdot (√(5))/(√(5)) = -(√(5))/(5)\\\\\cos \theta = (x)/(r) = (2)/(√(5)) \cdot (√(5))/(√(5)) = -(2√(5))/(5) \\\\\tan \theta = (y)/(x) = (-1)/(2) = -(1)/(2) \\\\\cot \theta = (x)/(y) = (2)/(-1) = -2\\\\\sec \theta = (r)/(x) = (√(5))/(2) \\\\\csc \theta = (r)/(y) = (√(5))/(-1) = -√(5)`