Answer:
Therefore the Volume of a Regular Tetrahedron of side 35 cm is
5028.87 cm³.
Explanation:
Regular Tetrahedron :
A regular tetrahedron is one in which all four faces are equilateral triangles.
There are a total of 6 edges in regular tetrahedron, all of which are equal in length. \
There are four vertices of regular tetrahedron, 3 faces meets at any one vertex.
Given:
Side = edge = a = 35 cm
To Find:
volume of a regular tetrahedron = ?
Solution:
Volume of a Regular Tetrahedron is given as
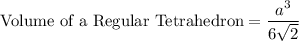
Where, a = edge
Substituting the values we get
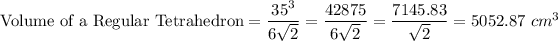
Therefore the Volume of a Regular Tetrahedron of side 35 cm is
5028.87 cm³.