Question

Two vertical springs have identical spring constants, but one has a ball of mass m hanging from it and the other has a ball of mass 2m hanging from it.Part A If the energies of the two systems are the same, what is the ratio of the oscillation amplitudes?

Answer 1

To solve this problem we will start from the definition of energy of a spring mass system based on the simple harmonic movement. Using the relationship of equality and balance between both systems we will find the relationship of the amplitudes in terms of angular velocities. Using the equivalent expressions of angular velocity we will find the final ratio. This is,

The energy of the system having mass m is,

`E_m = (1)/(2) m\omega_1^2A_1^2`

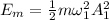
The energy of the system having mass 2m is,

`E_(2m) = (1)/(2) (2m)\omega_1^2A_1^2`

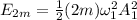
For the two expressions mentioned above remember that the variables mean

m = mass

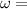`\omega =`Angular velocity

A = Amplitude

The energies of the two system are same then,

`E_m = E_(2m)`

`(1)/(2) m\omega_1^2A_1^2=(1)/(2) (2m)\omega_1^2A_1^2`

`(A_1^2)/(A_2^2) = (2\omega_2^2)/(\omega_1^2)`

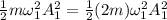
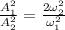
Remember that

`k = m\omega^2 \rightarrow \omega^2 = k/m`

Replacing this value we have then

`(A_1)/(A_2) = \sqrt{(2(k/m_2))/((k/m_1)^2)}`

`(A_1)/(A_2) = √(2) \sqrt{(m_1)/(m_1)}`

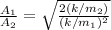
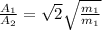
But the value of the mass was previously given, then

`(A_1)/(A_2) = √(2) \sqrt{(m)/(2m)}`

`(A_1)/(A_2) = √(2) \sqrt{(1)/(2)}`

`(A_1)/(A_2) = 1`

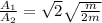
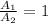
Therefore the ratio of the oscillation amplitudes it is the same.