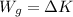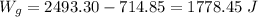Question

A projectile of mass 6.8 kg kg is shot horizontally with an initial speed of 14.5 m/s from a height of 26.7 m above a flat desert surface. The acceleration of gravity is 9.81 m/s². For the instant before the projectile hits the surface, find the work done on the projectile by gravity. Answer in units of J.

Answer 1

Step-by-step explanation:

Given

mass of projectile
`m=6.8\ kg`

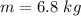
initial horizontal speed
`u_x=14.5\ m/s`

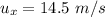
height
`h=26.7\ m`

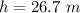
Considering vertical motion

velocity gained by projectile during 26.7 m motion

`v^2-u^2=2 as`

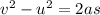
v=final velocity

u=initial velocity

a=acceleration

s=displacement

`v^2-(0)^2=2* (9.8)* (26.7)`

`v=√(523.32)`

`v=22.87\ m/s`

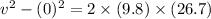
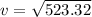
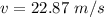
Horizontal velocity will remain same as there is no acceleration

final velocity
`v_(net)=√((v)^2+(u_x)^2)`

`v_(net)=√(733.57)=27.08\ m/s`

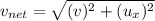
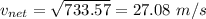
Initial kinetic Energy
`K_i=(1)/(2)mu_x^2`

`K_i=(1)/(2)* 6.8* (14.5)^2=714.85\ J`

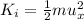
Final Kinetic Energy
`K_f=(1)/(2)mv_(net)^2`

`K_f=(1)/(2)* 6.8* (27.08)^2`

`K_f=2493.30\ J`

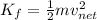
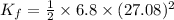
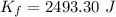
Work done by all the force is equal to change in kinetic Energy of object

Work done by gravity is
`W_g`

`W_g=\Delta K`

`W_g=2493.30-714.85=1778.45\ J`