Question

Solve x^2=2x+3 by factoring

Answer 1

The solution is x = 1 and x = -3

Solution:

Given that we have to solve the given equation by factoring

Given equation is:

`x^2=2x + 3\\\\x^2 - 2x - 3 = 0`

`\text{Consider the form } x^2+bx+c`

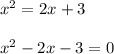
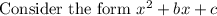
Find a pair of integers whose product is c and and whose sum is b

`\text{Compare } x^2-2x-3 = 0 \text{ with } x^2+bx +c\\\\\text{We get } b = -2 \text{ and } c = -3`

Now find, a pair of integers whose sum is -2 and product is -3

The integers that satisfies this condition is -1 and 3

When we add - 1 and 3 we get 2

When multiply -1 and 3 we get -3

Thus the pair of integers are -1 and 3

Write the factored form using these integers.

`(x-1)(x+3) = 0`

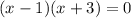
The Zero Product Property states that if ab = 0, then either a = 0 or b = 0, or both a and b are 0

Set the factors equal to 0

`x - 1 = 0 \text{ and } x + 3 = 0`

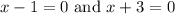
x = 1 and x = -3

Thus the solution is x = 1 and x = -3