Question

What are the solutions of the equation x4 – 5x2 – 14 = 0? Use factoring to solve.

x = plus-or-minus StartRoot 7 EndRoot and x = plus-or-minus StartRoot 2 EndRoot
x = plus-or-minus i StartRoot 7 EndRoot and x = plus-or-minus i StartRoot 2 EndRoot
x = plus-or-minus i StartRoot 7 EndRoot and x = plus-or-minus StartRoot 2 EndRoot
x = plus-or-minus StartRoot 7 EndRoot and x = plus-or-minus i StartRoot 2 EndRoot

Answer 1

Answer: D

Step-by-step explanation: Edge2023

Answer 2

`\left \{ {{x_(1) =+√(7) } \atop {x_(2) =-√(7)}} \right.`

`\left \{ {{x_(3) =+√(2)i } \atop {x_(4) =-√(2)i}} \right.`

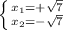
Explanation:

The given equation is

`x^(4)-5x^(2) -14=0`

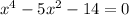
To factor this expression, we can change variables to make easier to see the solution.

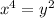`x^(4)=y^(2)` and
`x^(2) = y`

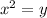
Applying the change, we have

`y^(2)-5y-14=0`

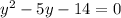
Now, you can observe that to factor this expression, we just need to find two number which product is 14 and which difference is 5, such numbers are 7 and 2.

`y^(2)-5y-14=(y-7)(y+2)`

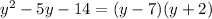
However, remember that
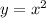`y=x^(2)`, so

`x^(4)-5x^(2) -14=(x^(2)-7 )(x^(2)+2)=0`

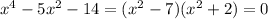
Applying the zero property, we have

`x^(2) -7=0 \implies x^(2) =7 \implies \left \{ {{x_(1) =+√(7) } \atop {x_(2) =-√(7)}} \right.`

`x^(2) +2=0 \implies x^(2) =-2 \implies \left \{ {{x_(3) =+√(2)i } \atop {x_(4) =-√(2)i}} \right.`

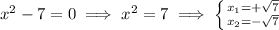
As you can see, the equation has two real solutions and two complex solutions.

Therefore, the right answer is the last choice.