Answer:
16.52 lb NaCl will be in the tank at the end of 3 hours.
Step-by-step explanation:
Let s(t) = gal of NaCl in a container at time t (in minutes).
s'(t) = The rate at which the amount of gal of NaCl in the container is changing.
s'(t) = Rate of NaCl going in - Rate of NaCl going out
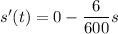
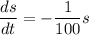
By variable separable method we get
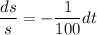
Integrate both sides.
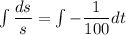

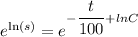
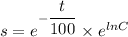

![[\because e^(\ln x)=x]](https://img.qammunity.org/2021/formulas/chemistry/high-school/wy0ekkvdaqe62ifishkfstm2q7xxlm6psh.png)
100 Ib of NaCl are initially dissolved in 600 gal of a NaCl solution in a container. it means s(0)=100.
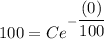
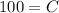
Therefore the required function is
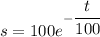 .... (1)
.... (1)
We need to find the amount of NaCl will be in the tank at the end of 3 hours.
3 hours = 180 minutes.
Substitute t=180 in equation (1).
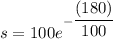

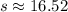
Therefore, 16.52 lb NaCl will be in the tank at the end of 3 hours.