Question

Determine algebraically whether the function is even, odd, or neither even nor odd.

f(x) = 3x^2 - 1
Neither
Even
Odd

Answer 1

Given Function is an even function

Explanation:

Explanation:-

Even function :-

A function f is even if the graph of f is symmetric with respective to the y - axis.

Algebraically, f is even if and only if f(-x) = f(x) for all x in the domain of f.

Odd function : -

A function f is odd if the graph of f is symmetric with respective to the origin

Algebraically, f is odd if and only if f(-x) = - f(x) for all x in the domain of f.

given function is
`f(x) = 3 x^2-1`

`f(-x) = 3 (-x)^2-1=3 x^2 -1 = f(x)`

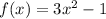
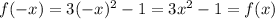
therefore f(-x) = f(x)

given function is an even function.