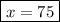Answer:
x=75
Explanation:
Solving Logarithm Equations
The natural logarithm is the inverse function of the exponential function which means
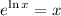
We have this equation to solve for x
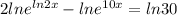
Applying the above property
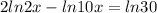
Also knowing that
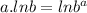
We have
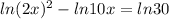
Using the fundamental property of logarithms
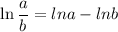
We reduce:
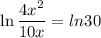
Taking off logarithms
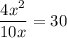
Operating
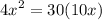
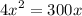
Dividing by x (assuming x different from 0)
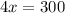
Solving