Question

Information is given about a polynomial f(x) whose coefficients are real numbers. Find the remaining zeros of f.

Degree 6; zeros: -1, 2 + i, -3 - i, 0

Answer 1

The remaining zeros of f is (2 - i) and (-3 + i).

Explanation:

We are given a degree six polynomial f and four of its zeros:

`\displaystyle x = -1, 2+i, -3-i, 0`

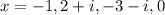
And we want to find the remaining zeros of f.

By the Fundamental Theorem of Algebra, the number of zeros of any polynomial is equal to its degree.

Hence, a sixth degree polynomial must have six zeros.

Because we are given four zeros, f has two more zeros.

To find the remaining two zeros, recall the Complex Conjugate Root Theorem:

`\displaystyle \text{If } a+bi \text{ is a zero, then } a-bi\text{ is also a zero.}`

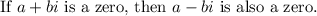
Our two complex zeros are (2 + i) and (-3 - i).

Then by the above theorem, (2 - i) and (-3 + i) is the two remaining zeros of f.