Question

Rationalize denominator when a monomial is in the denominator.Please show steps

Answer 1

`\frac{\sqrt[3]{90 x^2 y z^2} }{6 y z}`

Explanation:

step 1;-

Given
`\frac{\sqrt[3]{5 x^2} }{\sqrt[3]{12 y^2 z} }`

now you have rationalizing denominator (i.e monomial) with

`\frac{\sqrt[3]{5 x^2} }{\sqrt[3]{12 y^2 z} } X \frac{\sqrt[3]{(12 y^2 z)^(2) } }{\sqrt[3]{(12 y^2 z)^2} }`

By using algebraic formula is

• 
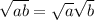  `√(ab) = √(a) √(b)`......(a)

• now
  `\frac{\sqrt[3]{5 x^2)(12 y^2 z)^2} }{\sqrt[3]{12 y^2 z)(12 y^2 z)^2} }`

• 
  `\frac{\sqrt[3]{720 x^2 y^4 z^2} }{\sqrt[3]{(12 y^2 z)^(3) } }`....(1)

• again using Formula
  `\sqrt[n]{a^(n) } =a`

now simplification , we get denominator function

• 
  `\frac{\sqrt[3]{720 x^2 y^4 z^2} }{12 y^2 z}`

again you have to simplify numerator term

• 
  `\frac{\sqrt[3]{2^3 y^3 90 (x^2  y z^2)} }{12 y^2 z}`

now simplify

• 
  `\frac{2 y\sqrt[3]{90 x^2 y  z^2} }{12 y^2 z}`

cancelling y and 2 values

we get Final answer

`\frac{\sqrt[3]{90 x^2 y z^2} }{6 y z}`