Question

Beth sells candles from her website. She can get a candle from her suppliers at a cost of $3 to her. The candles have been selling for $5, and at this price, consumers have been buying a steady 4000 per month. Beth would like to raise prices, but a market surveyor told her that for each increase of $1 in the price of an candle, she would lose 300 more sales each month. At what price should she sell the candles to maximize her profit?

Answer 1

$10.67

Step-by-step explanation:

Data provided in the question:

Initial cost = $3

Initial selling cost = $5

Initial sales = 4000

with $1 increase in price she loses 300 sales per month

Now,

Let the increase in price which maximizes the profit be '$x'

Therefore,

Final selling price = $5 + x

Final sales = 4000 - 300x

Thus,

Revenue = Final selling price × Final sales

= ( 5 + x)( 4000 - 300x)

= 20,000 - 1500x + 4000x - 300x²

= 20,000 + 2500x - 300x²

Total Cost = Initial cost × Final sales

= 3(4000 - 300x )

= 12,000 - 900x

Now,

Profit = Total revenue - Total cost

or

P = [ 20,000 + 2500x - 300x² ] - [ 12,000 - 900x ]

or

P = 8,000 + 3400x - 300x²

for point of maxima
`(dP)/(dx)=0`

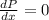
Thus,

0 = 0 + 3400 - 300(2x)

or

0 = 3400 - 600x

or

600x = 3400

or

x =
`(17)/(3)`

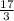
Hence,

The price will be = $5 + x =
`5 + (17)/(3)`

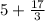
= $10.67