Question

A uniform, solid metal disk of mass 6.10 kgkg and diameter 30.0 cmcm hangs in a horizontal plane, supported at its center by a vertical metal wire. You find that it requires a horizontal force of 4.29 NN tangent to the rim of the disk to turn it by 3.40 ∘∘, thus twisting the wire. You now remove this force and release the disk from rest.

Answer 1

10.84406 Nm/rad

0.068625 kgm²

2.00066 rad/s

0.49983 s

Step-by-step explanation:

F = Force = 4.29 N

R = Radius =
`(30)/(2)=15\ cm`

`\theta` = Angle =
`3.4\ ^(\circ)`

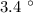
m = Mass of disk = 6.1 kg

Torsional constant is given by

`J=(\tau)/(\theta)\\\Rightarrow J=(FR)/(\theta)\\\Rightarrow J=(4.29* 0.15)/(3.4* (\pi)/(180))\\\Rightarrow J=10.84406\ Nm/rad`

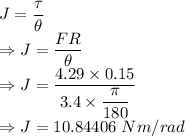
The torsion constant is 10.84406 Nm/rad

Moment of inertia is given by

`I=(1)/(2)mr^2\\\Rightarrow I=(1)/(2)6.1* 0.15^2\\\Rightarrow I=0.068625\ kgm^2`

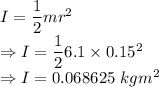
The moment of inertia is 0.068625 kgm²

Frequency is given by

`f=(1)/(2\pi)\sqrt{(J)/(I)}\\\Rightarrow f=(1)/(2\pi)\sqrt{(10.84406)/(0.068625)}\\\Rightarrow f=2.00066\ rad/s`

The frequency is 2.00066 rad/s

Time period is given by

`T=(1)/(f)\\\Rightarrow T=(1)/(2.00066)\\\Rightarrow T=0.49983\ s`

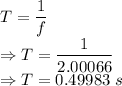
The time period is 0.49983 s