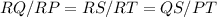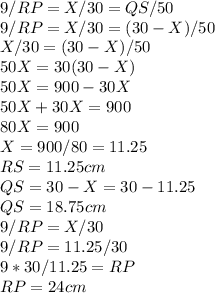QP=24 cm
RS=11.25 cm
QS=18.75 cm
Step-by-step explanation:
Given that TQ bisects <RTP
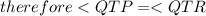 (1)
(1)
consider ΔRQS and ΔRPT
QS||PT,RP and RT are transversals
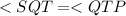 (alternate angles)(2)
(alternate angles)(2)
comparing (1) and (2)
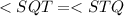 and triangle SQT is isocelus
and triangle SQT is isocelus
Therefore SQ=ST(sides opposite to equal angles in an isocelus triangle)
Therefore <RQS=<RPT(corresponding angles)
<RSQ=<RTP(corresponding angles)
therefore by AA criterion for similarity
ΔRQS~ΔRPT
According to the property of similar triangles