Question

This year the senior class at High School A and the senior class at High School B both planned trips there. The senior class at High School A rented and filled 11 vans and 9 buses with 624 students. High School B rented and filled 5 vans and 1 bus with 126 students. Each van and each bus carried the same number of students. Find the number of students in each van and in each bus.

Answer 1

There were 15 students in van and 51 students in the bus.

Explanation:

Let the number of students in each van be 'x'.

Let the number of students in each bus be 'y'.

Given:

For High School A

number of vans = 11

Number of buses =9

Number of students = 624

now we can say that;

Total Number of students is equal to sum of the number of vans multiplied by the number of students in each van and Number of buses multiplied by the number of students in each bus.

framing in equation form we get;

`11x+9y = 624 \ \ \ \ equation\ 1`

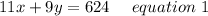
For High School B

number of vans = 5

Number of buses = 1

Number of students = 126

now we can say that;

Total Number of students is equal to sum of the number of vans multiplied by the number of students in each van and Number of buses multiplied by the number of students in each bus.

framing in equation form we get;

`5x+y = 126 \ \ \ \ equation\ 2`

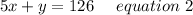
On solving both equation we will get the number of students in vans and buses.

First we will multiply equation 2 by 9 we get;

`9(5x+y)=126* 9\\\\45x+9y = 1134 \ \ \ \ equation\ 3`

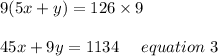
Now Subtracting equation 2 from equation 1 we get;

`45x+9y-(11x+9y)=1134-624\\\\45x+9y-11x-9y = 510\\\\34x=510`

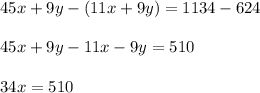
Now dividing both side by 34 we get;

`(34x)/(34)=(510)/(34)\\\\x= 15`

Now we will substitute the value of 'x' in equation 2 we get;

`5x+y=126\\\\5*15+y=126\\\\75+y =126\\\\y=126-75 = 51`

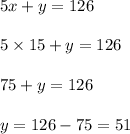
Hence There were 15 students in van and 51 students in the bus.