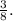Question

An experiment involves flipping a coin three times.

The following tree diagram shows the possible outcomes for the experiment.


What is the probability of getting exactly 2 tails?

Enter your answer as a reduced fraction, like this: 3/14

Answer 1

2⋅2⋅2=8 possible combinations in total.

Explanation:

Answer 2

The probability of getting exactly two tails in three coin flips is
`\( (3)/(8) \).`

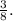
The image you've provided likely shows a tree diagram for the outcomes of flipping a coin three times. Each branch of the tree diagram represents the outcome of one coin flip, with "H" representing heads and "T" representing tails.

To calculate the probability of getting exactly two tails (T) in three coin flips, follow these steps:

1. Identify all the branches of the tree diagram that result in exactly two tails and one head.

2. Calculate the probability of each individual branch, which is \( \frac{1}{2} \) for heads and
`\( (1)/(2) \)` for tails on each flip, since a fair coin has an equal chance of landing heads or tails.

3. Since each flip is independent, multiply the probabilities along the branches to get the probability of that specific outcome.

4. Add up the probabilities of all the branches that result in exactly two tails.

Since the tree diagram is not visible to me, I will assume a fair coin and a standard tree diagram for three coin flips. There are three unique outcomes that result in exactly two tails: HTT, THT, and TTH. Each of these outcomes has the same probability of occurring:

`\[ \text{Probability of HTT} = (1)/(2) * (1)/(2) * (1)/(2) = (1)/(8) \]`

`\[ \text{Probability of THT} = (1)/(2) * (1)/(2) * (1)/(2) = (1)/(8) \]`

`\[ \text{Probability of TTH} = (1)/(2) * (1)/(2) * (1)/(2) = (1)/(8) \]`

Adding these probabilities together:

\
`\text{Total probability for exactly two tails}` =
`(1)/(8) + (1)/(8) + (1)/(8) = (3)/(8)`

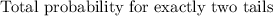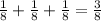
So, the probability of getting exactly two tails in three coin flips is
`\( (3)/(8) \).`