Question

The county fair is a popular field trip destination. This year the senior class at High School A and the senior class at High School B both planned trips there. The senior class at High School A rented and filled 11 vans and 9 buses with 624 students. High School B rented and filled 5 vans and 1 bus with 126 students. Each van and each bus carried the same number of students. Find the number of students in each van and in each bus.

Answer 1

15 students are in each van and 51 students are in each bus

Solution:

Let "x" be the number of students in each van

Let "y" be the number of students in each bus

The senior class at High School A rented and filled 11 vans and 9 buses with 624 students

Therefore, a equation is framed as:

11 vans x number of students in each van + 9 buses x number of students in each bus = 624

`11 * x + 9 * y = 624`

11x + 9y = 624 ------- eqn 1

High School B rented and filled 5 vans and 1 bus with 126 students

Therefore, a equation is framed as:

5 vans x number of students in each van + 1 buses x number of students in each bus = 126

`5 * x + 1 * y = 126`

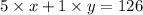
5x + y = 126 ---------- eqn 2

Let us solve eqn 1 and eqn 2

From eqn 2,

y = 126 - 5x ------ eqn 3

Substitute eqn 3 in eqn 1

11x + 9(126 - 5x) = 624

11x + 1134 - 45x = 624

-34x = 624 - 1134

-34x = -510

34x = 510

x = 15

Substitute x = 15 in eqn 3

y = 126 - 5(15)

y = 126 - 75

y = 51

Thus 15 students are in each van and 51 students are in each bus