Answer:
Option C. 16
Explanation:
Number of differents colors = 4
Number of differents sizes = 2
Case 1: 3 notepads of the same size and the same color:
If we have a package with the same size and the same color, the number of possible packages is:
N° packages = 4(colors)*2(sizes) = 8
Case 2: 3 notepads of the same size and different colors:
In this case, to calculate the number of possible permutations of packages without repetitions we need to use the following equation:
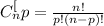
where p: is the number of colors for each package = 3, and n: is the total number of colors = 4.
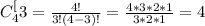
This number calculated is for one size, if the have two different sizes the number of possible packages is:
N° packages = 4(colors)*2(sizes) = 8
Therefore, the total number of different possible packages is:
N° packages = case 1 + case 2 = 8 + 8 = 16
So, the correct answer is option C = 16.
I hope it helps you!