Question

Write an inequality for x that would give this rectangle a perimeter of at least 300ft

Width:3ft
Height:x+5ft

Answer 1

The inequality for
`x` is:

`x\geq 142`

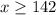
Explanation:

Given:

Width of rectangle = 3 ft

Height or length of rectangle =
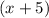`(x+5)` ft

Perimeter is at least 300 ft

To write an inequality for
`x`.

Solution:

Perimeter of a rectangle is given as:

⇒
`2l+2w`

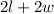
where
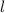`l` represents length of the rectangle and
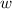`w` represents the width of the rectangle.

Plugging in the given values in the formula, the perimeter can be given as:

⇒
`2(x+5)+2(3)`

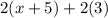
Using distribution:

⇒
`2x+10+6`

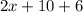
Simplifying.

⇒
`2x+16`

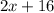
The perimeter is at lest 300 ft. So, the inequality can be given as:

⇒
`2x+16\geq 300`

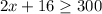
Solving for
`x`

Subtracting both sides by 16.

⇒
`2x+16-16\geq 300-16`

⇒
`2x\geq284`

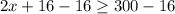
Dividing both sides by 2.

⇒
`(2x)/(2)\geq (284)/(2)`

⇒
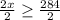
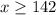`x\geq 142` (Answer)