Question

A 1720 kg car skidding due north on a level frictionless icy road at 239.44 km/h collides with a 2597.2 kg car skidding due east at 164 km/h in such a way that the two cars stick together. 2597.2 kg 164 km/h 239.44 km/h 1720 kg vf θ N At what angle (−180◦ ≤ θ ≤ +180◦ ) East of North do the two coupled cars skid off at? Answer in units of ◦ .

Answer 1

`\theta=44.03^(o)`

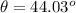
Explanation:

Here we have an inelastic collision problem. We can use the momentum (p = mv) conservation law in each component of the displacement.

So,
`p_(i)=p_(f)`

X-component:

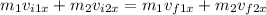`m_(1)v_(i1x)+m_(2)v_(i2x)=m_(1)v_(f1x)+m_(2)v_(f2x)` (1)

Now,

• v(i1x) is 0, because the first car just moving in y-direction
• v(i2x) is 164 km/h
• v(f1x)=v(f2x), because both cars stick together after the collision, so they have the same x-component velocity.

Then, using this information we can rewrite the equation (1).

`m_(2)v_(i2x)=v_(fx)(m_(1)+m_(2))`

`v_(fx)=(m_(2)v_(i2x))/(m_(1)+m_(2))=(2597.2*164)/(1720+2597.2)`

`v_(fx)=98.66 km/h`

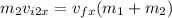
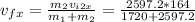
Y-component:

`m_(1)v_(i1y)+m_(2)v_(i2y)=m_(1)v_(f1y)+m_(2)v_(f2y)` (2)

We can do the same but with the next conditions:

• v(i1y) is 239.44 km/h
• v(i2y) is 0, because the second car just moving at the x-direction
• v(f1y)=v(f2y), because both cars stick together after the collision, so they have the same y-component velocity.

Then, using this information we can rewrite the equation (2).

`m_(1)v_(i1y)=v_(fy)(m_(1)+m_(2))`

`v_(fy)=(m_(1)v_(i1y))/(m_(1)+m_(2))=(1720*239.44)/(1720+2597.2)`

`v_(fy)=95.39 km/h`

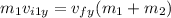
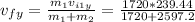
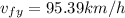
Now, as we have both components of the final velocity, we can find the angle East of North. Using trigonometric functions, we have:

`tan(\theta)=(v_(y))/(v_(x))`

`\theta=arctan((v_(y))/(v_(x)))=arctan((95.39)/(98.66))`

`\theta=44.03^(o)`

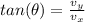
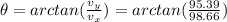
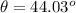
I hope it helps you!